矩阵特征多项式的展开

天大的线性代数教材上有这样一则命题：

命题 1

数域 $\mathbb{P}^n$ 上的 $n \times n$ 矩阵 $\boldsymbol{A} = [a_{ij}]_{n \times n}$，其特征多项式 $f(\lambda)= \left| \lambda I_n - \boldsymbol{A} \right|$ 可以表示为：

$$ f(\lambda)=\lambda ^n - \mathrm{tr}(\boldsymbol{A}) \lambda ^{n-1} + \cdots + \left( -1 \right) ^n \det(\boldsymbol{A}) \tag{1} $$

书上给予了此式的证明。

那中间这些省略的中间的项又都是多少呢？？

我们可以尝试找出规律：

我使用 Python 的符号计算尝试找出了以下规律：

from sympy import *
import sys

x=Symbol('x')
vars = [symbols('a_1:4'),symbols('b_1:4'),symbols('c_1:4')]
M1 = Matrix([[x-vars[0][0], -vars[0][1] ,-vars[0][2]], \
             [-vars[1][0], x-vars[1][1], -vars[1][2]], \
             [-vars[2][0], -vars[2][1], x-vars[2][2]]])
det(M1)

不难发现，在 $n=3$ 的情况下，特征多项式可表示为：

$$ f(\lambda)=\lambda ^3 - \mathrm{tr}\left(\boldsymbol{A}\right) \lambda ^{2} + \left( \sum_{i \ne j} a_{ii}a_{jj} - \sum_{i \ne j} a_{ij}a_{ji}\right) \lambda- \det \left(\boldsymbol{A}\right) $$

继续尝试 $n=4$ 时的情况：

B=Matrix(4,4,symbols('B:4:4')) #创建4*4的矩阵B
I=diag(x,x,x,x) #特征值x乘以单位矩阵
eig_B=I-B  # xI-B

eigen_poly=det(eig_B) # 特征多项式的展开
eigen_poly.coeff(x**3) #提取x^3项的系数
eigen_poly.coeff(x**2)  #提取x^2项的系数
eigen_poly.coeff(x) #提取x项的系数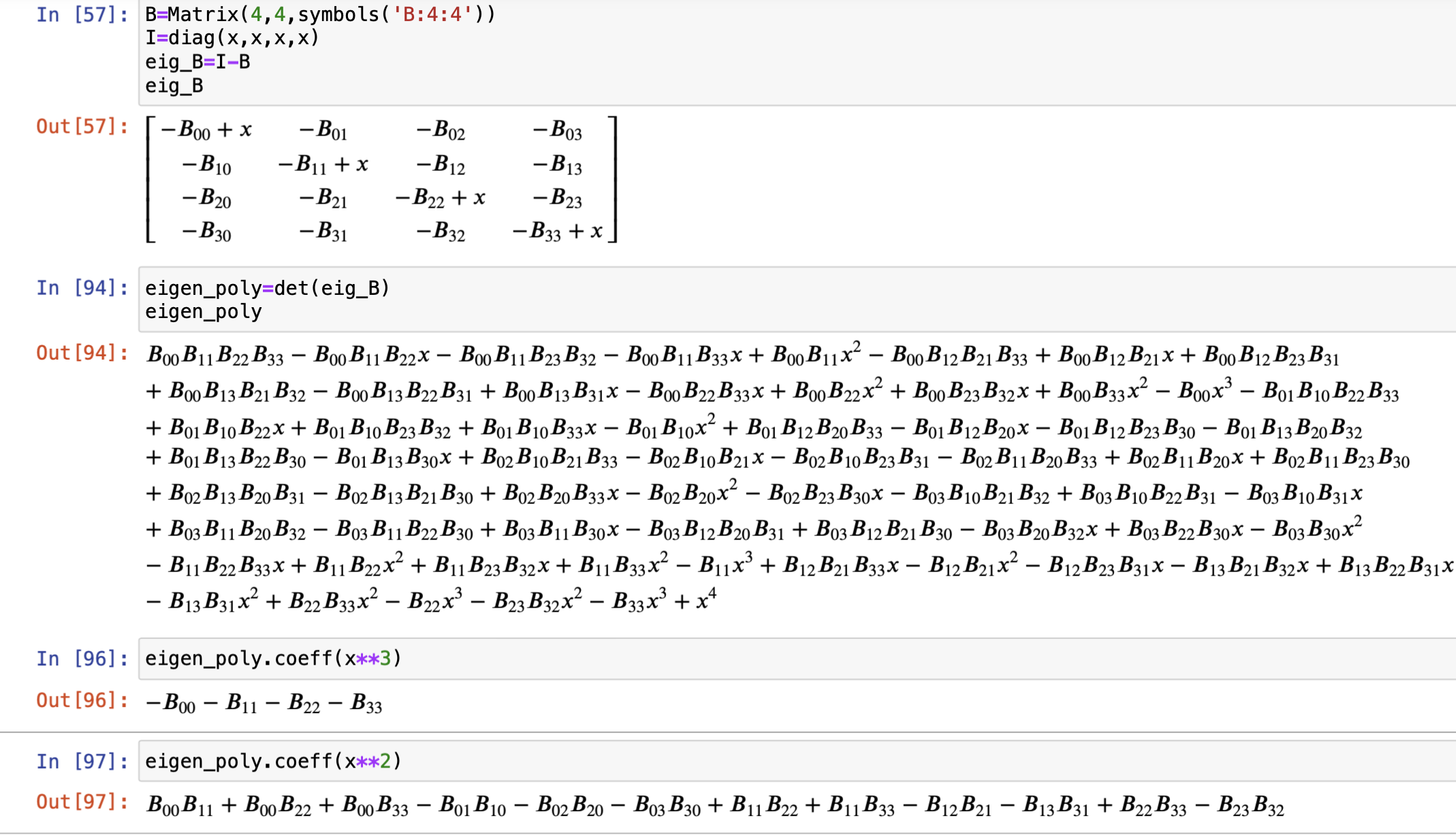

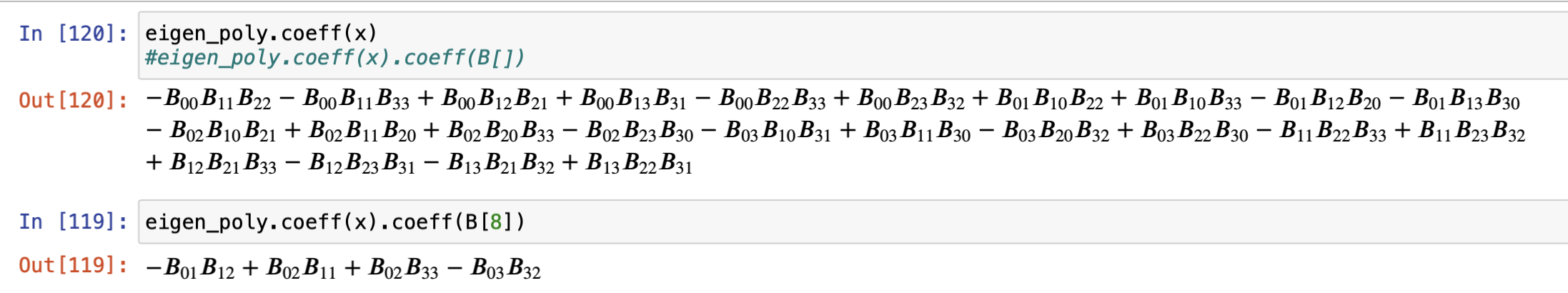
我们发现，4阶方阵的中间项也是满足某种规律的，就此提出以下命题。

命题2

数域 $\mathbb{P}^n$ 上的 $n \times n$ 矩阵 $\boldsymbol{A} = [a_{ij}]_{n \times n}$，其特征多项式 $f(\lambda)= \left| \lambda I_n - \boldsymbol{A} \right|$ 可以表示为：

$$ f(\lambda)=\lambda ^n - \mathrm{tr}(\boldsymbol{A}) \lambda ^{n-1} + \cdots + \left( -1 \right) ^n \det(\boldsymbol{A}) $$

由上面的计算得到的结果，我们发现，它可以进一步地写为：( $n=4$ 时)

$$ f(\lambda)=\lambda ^4 - \mathrm{tr}(\boldsymbol{A}) \lambda ^{3} + \sum_{1 \le \mu \lt \nu \le n } \left( a_{\mu \mu} a_{\nu \nu} \right )^{\mathrm{II}}\lambda^{2}- \sum_{1 \le \mu \le n } A_{\mu \mu}^{\mathrm{III}} \,\lambda^{1} + \det(\boldsymbol{A}) \tag{2} $$

• 其中：

  $\left( a_{\mu \mu} a_{\nu \nu} \right )^{\mathrm{II}}$ 表示4阶方阵 $A$ 中（不含有第 $\mu$ 行第 $\mu$ 列与第 $\nu$ 行第 $\nu$ 列）的二阶主子式；

  $A_{\mu \mu}^{\mathrm{III}}$ 表示 $A$ 中（不含有第 $\mu$ 行第 $\mu$ 列）的三阶主子式。

所谓“ $k$ 阶主子式”是我们临时定义的概念，可能与已经定义的概念相冲突。

下图分别展示了 $4 \times 4$ 矩阵 $B=[b_{ij}]$ 的所有二阶主子式，和三阶主子式：

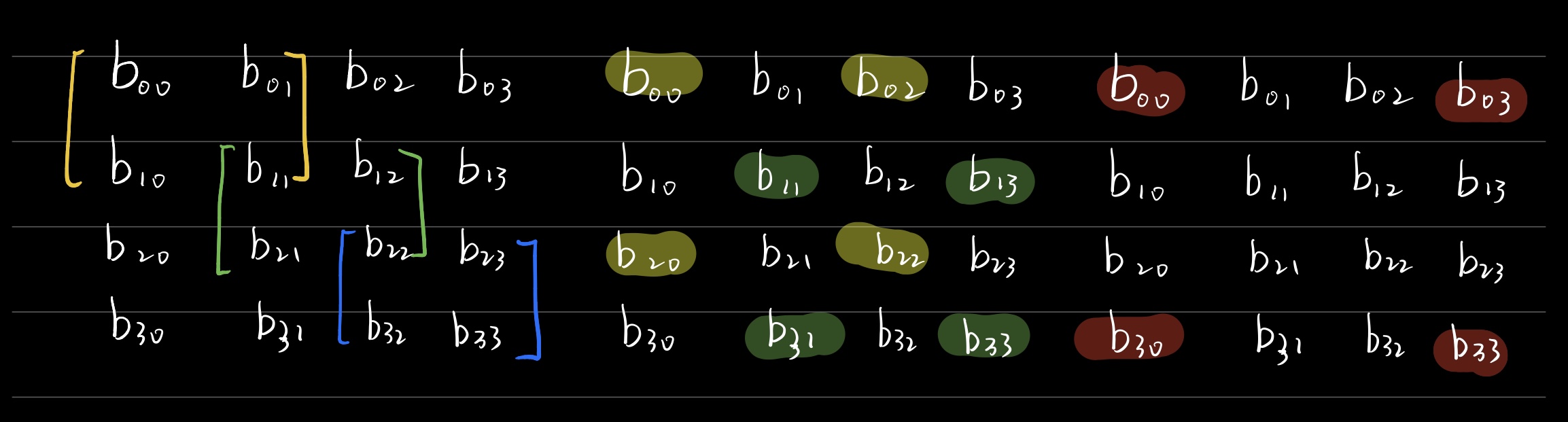
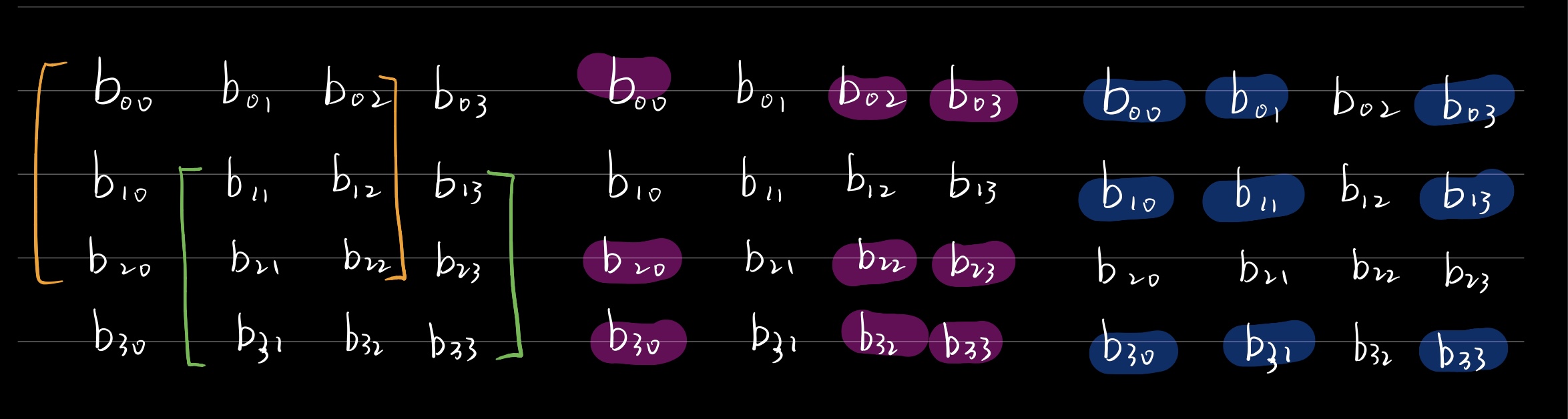
• 不难发现，整个 secular equation¹ 中 $\lambda ^{n-i}$ 项的系数，就是 $A$ 中所有 $i$ 阶主子式的和，再乘以系数 $(-1)^{i}$。

• 我们也同样可以发现：

  矩阵 $A$ 的迹 $\mathrm{tr}A$ 就是 $A$ 中所有一阶主子式的和（一共 $n$ 个）；

  行列式 $\det{A}$ 就是 $A$ 中所有 $n$ 阶主子式的和（只有一个）。

这样，我们推广到 $n$ 阶方阵上，就可以尝试把特征多项式写成：

$$ f(\lambda)=\lambda ^n - \mathrm{tr}(\boldsymbol{A}) \lambda ^{n-1} + \sum_{1 \le \mu \le n } A_{\mu \mu}^{\mathrm{II}}\lambda^{n-2}- \sum_{1 \le \mu \le n } A_{\mu \mu}^{\mathrm{III}} \,\lambda^{n-3} + \cdots + (-1)^{n-1} \sum_{1 \le \mu \le n } A_{\mu \mu}^{(\mathrm{n-1})} \,\lambda^{1} +(-1)^n\det(\boldsymbol{A}) \tag{3} $$

继续可以简化写成：

$$ f(\lambda)=\left | \lambda I_n -\boldsymbol{A} \right | =\sum_{i=0}^n (-1)^i \sum_\mu A_{\mu \mu}^{(i)} \,\lambda^{n-i} \tag{4} $$

其中 $\sum \limits _\mu A_{\mu \mu}^{(i)}$ 表示$A$ 中所有 $i$ 阶主子式的和，并定义 $\sum \limits_\mu A_{\mu \mu}^{(0)}=1$.

命题的证明就留给各位读者了。

3/18 更新

设 $\boldsymbol{A}$ 是一个 $m \times n$ 的矩阵，$I$ 是集合 ${1,\dots,m}$ 的一个 $k$ 元子集， $J$ 是集合 ${1,\dots,n}$ 的一个 $k$ 元子集，那么 $[\boldsymbol{A}]_{I,J}$ 表示 $\boldsymbol{A}$ 的 $k$ 阶子式。其中抽取的 $k$ 行的行标是 $I$ 中所有元素， $k$ 列的列标是 $J$ 中所有元素。²

• 若 $I=J$，则称 $[\boldsymbol{A}]_{I,J}$ 为 $\boldsymbol{A}$ 的 $k$ 阶主子式（principal minor）
• 如果 $I=J={1,\dots,k}$（所取的是左起前 $k$ 列和上起前 $k$ 行），那么相应的主子式被称为顺序主子式。一个 $n \times n$ 的方块矩阵有 $n$ 个顺序主子式（leading principal minors）。

子式的一个更为对称和代数化的定义可以通过多线性代数中的外积给出：k阶子式是k阶外幂的系数。

如果将矩阵的k列看做k个向量并在一起，那么它的k阶子式就是k阶外幂映射到的k-向量中的系数。²

Using the language of exterior algebra, the characteristic polynomial of an $n\times n$ matrix ${\displaystyle A}$ may be expressed as³

$$ p_{A}(t)=\sum _{k=0}^{n}t^{n-k}(-1)^{k}\mathrm{tr} \left(\textstyle \bigwedge ^{k}A\right) $$

where $\textstyle \mathrm{tr} \bigwedge^k A$ is the trace of the $k$ th exterior power of ${\displaystyle A}$ , which has dimension ${\binom {n}{k}}$.

This trace may be computed as the sum of all Principal minors of $\displaystyle A$ of size ${\displaystyle k}$ . The recursive Faddeev–LeVerrier algorithm computes these coefficients more efficiently.

When the characteristic) of the field) of the coefficients is $\displaystyle 0$, each such trace may alternatively be computed as a single determinant, that of the ${\displaystyle k\times k}$ matrix.

$$ {\displaystyle \operatorname {tr} \left(\textstyle \bigwedge ^{k}A\right)={\frac {1}{k!}}{\begin{vmatrix}\operatorname {tr} A&k-1&0&\cdots &\\\operatorname {tr} A^{2}&\operatorname {tr} A&k-2&\cdots &\\\vdots &\vdots &&\ddots &\vdots \\\operatorname {tr} A^{k-1}&\operatorname {tr} A^{k-2}&&\cdots &1\\\operatorname {tr} A^{k}&\operatorname {tr} A^{k-1}&&\cdots &\operatorname {tr} A\end{vmatrix}}~.} $$

参考资料